การหาจุดสูงสุดต่ำสุดของฟังก์ชั่นโดยวิธีลงไปทางที่ชันที่สุด Method of steepest descent สมัยนี้เรียก Gradient Descent

ในงานแยกแยะภาพ0-9 เราใช้ Neural Network เพื่อที่คุณจะเข้าใจ นิวรอลเน็ตเวิร์ค คุณต้องเข้าใจวิธีการหาจุดสูงสุดต่ำสุดเสียก่อน วิธีนี้เรียกว่าวิธีการหาจุดสูงสุดต่ำสุดด้วยทางที่ชันที่สุด ในปัญหาแยกแยะภาพ0-9นั้น การหาจุดสูงสุดต่ำสุดเป็นปัญหาการหาจุดสูงสุดของfunctionที่ทำแผนที่จาก 1024 ($\mathbb{R}^{1024}$) มิติสู่1มิติ($\mathbb{R}^1$) ซึ่งคนเราจินตนาการหรือเห็นพื้นผิวของฟังก์ชั่นใน1024 มิติไม่ได้ ดังนั้นจึุงต้องใช้วิธีการหาทางคณิตศาสตร์  และวิธีลงทางชันที่สุดเป็นหนึ่งในหลายวิธีเหล่านั้น

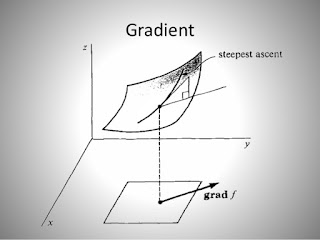
สมมุติว่าเรามี function $f(\mathbf{x})$ ของเรา ซึ่งสร้างแผนที่จาก $\mathbb{R}^2 \rightarrow \mathbb{R}^1$ ซึ่งแผนที่ที่ได้มีลักษณะเป็นโค้งพาราโบล่าดังรูป 

ถ้าเราต้องการหาจุดสูงสุดต่ำสุดของ function $z=f(\mathbf{x})$ของเรา จะทำได้อย่างไร
สังเกตุตัวหนาหมายถึงตัวแปรใน $\mathbb{R}^2$ ตัวบางแสดงถึงตัวแปรใน$\mathbb{R}^1$


 สมมุติว่าจุดศูนย์กลางการหมุนที่แตะกับพาราโบล่าเป็นจุด $\mathbf{x_0} = [x_0,y_0]$ การที่เราหา
$$\frac{\partial f}{\partial \mathbf{x}} = [\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}]$$ คำนวนที่ $\mathbf{x_0}$
 เราจะได้เส้นผ่านจุด $\mathbf{x_0}$    โปรดสังเกตุเส้นด้านล่างในรูปที่เขียนว่า grad f นั่นคือ $\partial f / \partial \mathbf{x}$ นั่นคือtangent ที่จะเคลื่อนที่ไปหาจุดสูงสุดคือtangent ที่ชันที่สุด   การหาค่า $\partial f / \partial \mathbf{x}$ทำให้เราได้ทิศทางใน $\mathbb{R}^2$ ที่ทำให้การเคลื่อนลงหรือขึ้นไปอย่างชันที่สุด

จากนั้นเราก็แค่เคลื่อนลงในกรณีหาจุดต่ำสุด เราเรียกว่า Gradient Descent

$$\begin{equation} do\\  \mathbf{x_0}^{next} = \mathbf{x_0} - a\frac{\partial f }{\partial \mathbf{x}}\biggr\rvert_{\mathbf{x_0}}\\ until \lbrace f(\mathbf{x_0}^{next}) - f(\mathbf{x_0}) \le \epsilon \rbrace \end{equation}$$

โดยที่ $a$ เป็นค่าคงที่จำนวนจริงบวก  เราเรียก $a$ ว่า Learning rate
หรือเคลื่อนขี้นในกรณีหาจุดสูงสุด เราเียกว่า Gradient Ascent

$$\mathbf{x_0}^{next} = \mathbf{x_0} +a \frac{\partial f }{\partial \mathbf{x}}\biggr\rvert_{\mathbf{x_0}}$$

นี่คือพื้นฐานที่สุดของ Neural Network นิวรอล เน็ตเวิร์ค   ถ้าฟังก์ชั่นของคุณเป็น convex function แล้ว วิธีการนี้การันตี Global Optimum

ผลของการลงไปทางที่ชันที่สุด   จุดสีแดงแสดงค่า $f(\mathbf{x_0})$ ในแต่ละรอบ